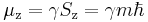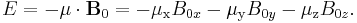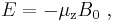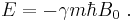Nuclear magnetic resonance

World's First 1 GHz NMR Spectrometer (1000 MHz, 23.5 T) was installed at the new ‘Centre de RMN à Très Hauts Champs’ in Lyon, France in August 2009
Pacific Northwest National Laboratory's high magnetic field (800 MHz, 18.8 T) NMR spectrometer.

Nuclear magnetic resonance (NMR) is a property that magnetic nuclei have in a magnetic field and applied electromagnetic (EM) pulse or pulses, which cause the nuclei to absorb energy from the EM pulse and radiate this energy back out. The energy radiated back out is at a specific resonance frequency which depends on the strength of the magnetic field and other factors. This allows the observation of specific quantum mechanical magnetic properties of an atomic nucleus. Many scientific techniques exploit NMR phenomena to study molecular physics, crystals and non-crystalline materials through NMR spectroscopy. NMR is also routinely used in advanced medical imaging techniques, such as in magnetic resonance imaging (MRI).

All stable isotopes that contain an odd number of protons and/or of neutrons (see Isotope) have an intrinsic magnetic moment and angular momentum, in other words a nonzero spin, while all nuclides with even numbers of both have spin 0. The most commonly studied nuclei are 1H (the most NMR-sensitive isotope after the radioactive 3H) and 13C, although nuclei from isotopes of many other elements (e.g. 2H, 10B, 11B, 14N, 15N, 17O, 19F, 23Na, 29Si, 31P, 35Cl, 113Cd, 129Xe, 195Pt) are studied by high-field NMR spectroscopy as well.

A key feature of NMR is that the resonance frequency of a particular substance is directly proportional to the strength of the applied magnetic field. It is this feature that is exploited in imaging techniques; if a sample is placed in a non-uniform magnetic field then the resonance frequencies of the sample's nuclei depend on where in the field they are located. Since the resolution of the imaging technique depends on the magnitude of magnetic field gradient, many efforts are made to develop increase field strength, often using superconductors. The effectiveness of NMR can also be improved using hyperpolarization, and/or using two-dimensional, three-dimensional and higher dimension multi-frequency techniques.

The principle of NMR usually involves two sequential steps:

The two fields are usually chosen to be perpendicular to each other as this maximizes the NMR signal strength. The resulting response by the total magnetization (M) of the nuclear spins is the phenomenon that is exploited in NMR spectroscopy and magnetic resonance imaging. Both use intense applied magnetic fields (H0) in order to achieve dispersion and very high stability to deliver spectral resolution, the details of which are described by chemical shifts, the Zeeman effect, and Knight shifts (in metals).

NMR phenomena are also utilized in low-field NMR, NMR spectroscopy and MRI in the Earth's magnetic field (referred to as Earth's field NMR), and in several types of magnetometers.

Contents

History

Discovery

Nuclear magnetic resonance was first described and measured in molecular beams by Isidor Rabi in 1938,[1] and in 1944, Rabi was awarded the Nobel Prize in physics for this work.[2] In 1946, Felix Bloch and Edward Mills Purcell expanded the technique for use on liquids and solids, for which they shared the Nobel Prize in physics in 1952.[3]

Purcell had worked on the development and radar applications during World War II at Massachusetts Institute of Technology's Radiation Laboratory. His work during that project on the production and detection of RF energy, and on the absorption of such RF energy by matter, preceded his discovery of NMR.

They noticed that magnetic nuclei, like 1H and 31P, could absorb RF energy when placed in a magnetic field of a strength specific to the identity of the nuclei. When this absorption occurs, the nucleus is described as being in resonance. Different atomic nuclei within a molecule resonate at different (radio) frequencies for the same magnetic field strength. The observation of such magnetic resonance frequencies of the nuclei present in a molecule allows any trained user to discover essential, chemical and structural information about the molecule.

The development of nuclear magnetic resonance as a technique of analytical chemistry and biochemistry parallels the development of electromagnetic technology and its introduction into civilian use.

Theory of nuclear magnetic resonance

Nuclear spin and magnets

All nucleons, that is neutrons and protons, composing any atomic nucleus, have the intrinsic quantum property of spin. The overall spin of the nucleus is determined by the spin quantum number S. If the number of both the protons and neutrons in a given nuclide are even then S = 0, i.e. there is no overall spin; just as electrons pair up in atomic orbitals, so do even numbers of protons or even numbers of neutrons (which are also spin-1⁄2 particles and hence fermions) pair up giving zero overall spin.

However, a proton and neutron will have lower energy when their spins are parallel, not anti-parallel, as this parallel spin alignment does not infringe upon the Pauli principle, but instead has to do with the quark structure of these two nucleons. Therefore, the spin ground state for the deuteron (the deuterium nucleus, or the 2H isotope of hydrogen)—that has only a proton and a neutron—corresponds to a spin value of 1, not of zero; the single, isolated deuteron is therefore exhibiting an NMR absorption spectrum characteristic of a quadrupolar nucleus of spin 1, which in the 'rigid' state at very low temperatures is a characteristic ('Pake') doublet, (not a singlet as for a single, isolated 1H, or any other isolated fermion or dipolar nucleus of spin 1/2). On the other hand, because of the Pauli principle, the (radioactive) tritium isotope has to have a pair of anti-parallel spin neutrons (of total spin zero for the neutron spin couple), plus a proton of spin 1/2; therefore, the character of the tritium nucleus ('triton') is again magnetic dipolar, not quadrupolar—like its non-radioactive deuteron neighbor, and the tritium nucleus total spin value is again 1/2, just like for the simpler, abundant hydrogen isotope, 1H nucleus (the proton). The NMR absorption (radio) frequency for tritium is however slightly higher than that of 1H because the tritium nucleus has a slightly higher gyromagnetic ratio than 1H. In many other cases of non-radioactive nuclei, the overall spin is also non-zero. For example, the 27Al nucleus has an overall spin value S = 5⁄2.

A non-zero spin is thus always associated with a non-zero magnetic moment (μ) via the relation μ = γS, where γ is the gyromagnetic ratio. It is this magnetic moment that allows the observation of NMR absorption spectra caused by transitions between nuclear spin levels. Most nuclides (with some rare exceptions) that have both even numbers of protons and even numbers of neutrons, also have zero nuclear magnetic moments-and also have zero magnetic dipole and quadrupole moments; therefore, such nuclides do not exhibit any NMR absorption spectra. Thus, 18O is an example of a nuclide that has no NMR absorption, whereas 13C, 31P, 35Cl and 37Cl are nuclides that do exhibit NMR absorption spectra; the last two nuclei are quadrupolar nuclei whereas the preceding two nuclei (13C and 31P) are dipolar ones.

Electron spin resonance (ESR) is a related technique which detects transitions between electron spin levels instead of nuclear ones. The basic principles are similar; however, the instrumentation, data analysis and detailed theory are significantly different. Moreover, there is a much smaller number of molecules and materials with unpaired electron spins that exhibit ESR (or electron paramagnetic resonance (EPR)) absorption than those that have NMR absorption spectra. Significantly also, is the much greater sensitivity of ESR and EPR in comparison with NMR. Furthermore, ferromagnetic materials and thin films may exhibit 'very unusual', highly resolved ferromagnetic resonance (FMR) spectra, or ferromagnetic spin wave resonance (FSWR) excitations in non-crystalline solids such as ferromagnetic metallic glasses, well beyond the common single-transitions of most routine NMR, FMR and EPR studies.[4][5]

Values of spin angular momentum

The angular momentum associated with nuclear spin is quantized. This means both that the magnitude of angular momentum is quantized (i.e. S can only take on a restricted range of values), and also that the orientation of the associated angular momentum is quantized. The associated quantum number is known as the magnetic quantum number, m, and can take values from +S to −S, in integer steps. Hence for any given nucleus, there is a total of 2S + 1 angular momentum states.

The z-component of the angular momentum vector (S) is therefore Sz = mħ, where ħ is the reduced Planck constant. The z-component of the magnetic moment is simply:

\mu_\mathrm{z} = \gamma S_\mathrm{z} = \gamma m\hbar

Spin behavior in a magnetic field

Splitting of nuclei spin states in an external magnetic field

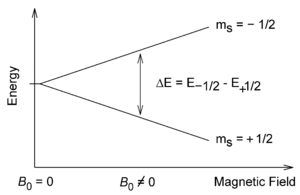
Consider nuclei which have a spin of one-half, like 1H, 13C or 19F. The nucleus has two possible spin states: m = 1⁄2 or m = −1⁄2 (also referred to as spin-up and spin-down, or sometimes α and β spin states, respectively). These states are degenerate, that is they have the same energy. Hence the number of atoms in these two states will be approximately equal at thermal equilibrium.

If a nucleus is placed in a magnetic field, however, the interaction between the nuclear magnetic moment and the external magnetic field mean the two states no longer have the same energy. The energy of a magnetic moment μ when in a magnetic field B0 is given by:

E = -\mathbf{\mu} \cdot \mathbf{B}_0 = -\mu_\mathrm{x} B_{0x}-\mu_\mathrm{y} B_{0y}-\mu_\mathrm{z} B_{0z} .

Usually the z axis is chosen to be along B0, and the above expression reduces to:

E = -\mu_\mathrm{z} B_0 \ ,

or alternatively:

E = -\gamma m\hbar B_0 \ .

As a result the different nuclear spin states have different energies in a non-zero magnetic field. In hand-waving terms, we can talk about the two spin states of a spin 1⁄2 as being aligned either with or against the magnetic field. If γ is positive (true for most isotopes) then m = 1⁄2 is the lower energy state.

The energy difference between the two states is:

\Delta{E} = \gamma \hbar B_0 \ ,

and this difference results in a small population bias toward the lower energy state.

Magnetic resonance by nuclei

Resonant absorption by nuclear spins will occur only when electromagnetic radiation of the correct frequency (e.g., equaling the Larmor precession rate) is being applied to match the energy difference between the nuclear spin levels in a constant magnetic field of the appropriate strength. The energy of an absorbed photon is then E = hν0, where ν0 is the resonance radiofrequency that has to match (that is, it has to be equal to) the Larmor precession frequency νL of the nuclear magnetization in the constant magnetic field B0. Hence, a magnetic resonance absorption will only occur when ΔE = hν0, which is when ν0 = γB0/(2π). Such magnetic resonance frequencies typically correspond to the radio frequency (or RF) range of the electromagnetic spectrum for magnetic fields up to ~20 T. It is this magnetic resonant absorption which is detected in NMR.

Nuclear shielding

It might appear from the above that all nuclei of the same nuclide (and hence the same g) would resonate at the same frequency. This is not the case. The most important perturbation of the NMR frequency for applications of NMR is the 'shielding' effect of the surrounding electrons. In general, this electronic shielding reduces the magnetic field at the nucleus (which is what determines the NMR frequency).

As a result the energy gap is reduced, and the frequency required to achieve resonance is also reduced. This shift in the NMR frequency due to the electrons' molecular orbital coupling to the external magnetic field is called chemical shift, and it explains why NMR is able to probe the chemical structure of molecules which depends on the electron density distribution in the corresponding molecular orbitals. If a nucleus in a specific chemical group is shielded to a higher degree by a higher electron density of its surrounding molecular orbital, then its NMR frequency will be shifted "upfield" (that is, a lower chemical shift), whereas if it is less shielded by such surrounding electron density, then its NMR frequency will be shifted "downfield" (that is, a higher chemical shift).

Unless the local symmetry of such molecular orbitals is very high (leading to "isotropic" shift), the shielding effect will depend on the orientation of the molecule with respect to the external field (B0). In solid-state NMR spectroscopy, magic angle spinning is required to average out this orientation dependence in order to obtain values close to the average chemical shifts. This is unnecessary in conventional NMR investigations of molecules, since rapid molecular tumbling averages out the chemical shift anisotropy (CSA). In this case, the term "average" chemical shift (ACS) is used.

Relaxation

The process called population relaxation refers to nuclei that return to the thermodynamic state in the magnet. This process is also called T1, "spin-lattice" or "longitudinal magnetic" relaxation, where T1 refers to the mean time for an individual nucleus to return to its thermal equilibrium state of the spins. Once the nuclear spin population is relaxed, it can be probed again, since it is in the initial, equilibrium (mixed) state.

The precessing nuclei can also fall out of alignment with each other (returning the net magnetization vector to a non-precessing field) and stop producing a signal. This is called T2 or transverse relaxation. Because of the difference in the actual relaxation mechanisms involved (for example, inter-molecular vs. intra-molecular magnetic dipole-dipole interactions ), T1 is always longer than T2 (that is, slower spin-lattice relaxation, for example because of smaller dipole-dipole interaction effects). In practice, the value of T*2 which is the actually observed decay time of the observed NMR signal, or free induction decay, (to 1/e of the initial amplitude immediately after the resonant RF pulse)-- also depends on the static magnetic field inhomogeneity, which is quite significant. (There is also a smaller but significant contribution to the observed FID shortening from the RF inhomogeneity of the resonant pulse). In the corresponding FT-NMR spectrum—meaning the Fourier transform of the free induction decay--the T*2 time is inversely related to the width of the NMR signal in frequency units. Thus, a nucleus with a long T2 relaxation time gives rise to a very sharp NMR peak in the FT-NMR spectrum for a very homogeneous ("well-shimmed") static magnetic field, whereas nuclei with shorter T2 values give rise to broad FT-NMR peaks even when the magnet is shimmed well. Both T1 and T2 depend on the rate of molecular motions as well as the gyromagnetic ratios of both the resonating and their strongly interacting, next-neighbor nuclei that are not at resonance.

NMR spectroscopy

Main article: NMR spectroscopy
900 MHz, 21.2 T NMR Magnet at HWB-NMR, Birmingham, UK

NMR spectroscopy is one of the principal techniques used to obtain physical, chemical, electronic and structural information about molecules due to either the chemical shift, Zeeman effect, or the Knight shift effect, or a combination of both, on the resonant frequencies of the nuclei present in the sample. It is a powerful technique that can provide detailed information on the topology, dynamics and three-dimensional structure of molecules in solution and the solid state. Thus, structural and dynamic information is obtainable (with or without "magic angle" spinning (MAS)) from NMR studies of quadrupolar nuclei (that is, those nuclei with spin S > 1⁄2) even in the presence of magnetic dipole-dipole interaction broadening (or simply, dipolar broadening) which is always much smaller than the quadrupolar interaction strength because it is a magnetic vs. an electric interaction effect.

Additional structural and chemical information may be obtained by performing double-quantum NMR experiments for quadrupolar nuclei such as 2H. Also, nuclear magnetic resonance is one of the techniques that has been used to design quantum automata, and also build elementary quantum computers.[6][7]

Continuous wave (CW) spectroscopy

In its first few decades, nuclear magnetic resonance spectrometers used a technique known as continuous-wave spectroscopy (CW spectroscopy). Although NMR spectra could be, and have been, obtained using a fixed magnetic field and sweeping the frequency of the electromagnetic radiation, this more typically involved using a fixed frequency source and varying the current (and hence magnetic field) in an electromagnet to observe the resonant absorption signals. This is the origin of the counterintuitive, but still common, "high" and "low" field terminology for low frequency and high frequency regions respectively of the NMR spectrum.

CW spectroscopy is inefficient in comparison to Fourier techniques (see below) as it probes the NMR response at individual frequencies in succession. As the NMR signal is intrinsically weak, the observed spectra suffer from a poor signal-to-noise ratio. This can be mitigated by signal averaging i.e. adding the spectra from repeated measurements. While the NMR signal is constant between scans and so adds linearly, the random noise adds more slowly—as the square-root of the number of spectra (see Random walk). Hence the overall ratio of the signal to the noise increases as the square-root of the number of spectra measured.

Fourier transform spectroscopy

Most applications of NMR involve full NMR spectra, that is, the intensity of the NMR signal as a function of frequency. Early attempts to acquire the NMR spectrum more efficiently than simple CW methods involved irradiating simultaneously with more than one frequency. A revolution in NMR occurred when short pulses of radio-frequency were used (centered at the middle of the NMR spectrum). In simple terms, a short square pulse of a given "carrier" frequency "contains" a range of frequencies centered about the carrier frequency, with the range of excitation (bandwidth) being inversely proportional to the pulse duration (the Fourier transform (FT) of an approximate square wave contains contributions from all the frequencies in the neighborhood of the principal frequency). The restricted range of the NMR frequencies made it relatively easy to use short (millisecond to microsecond) radiofrequency (RF) pulses to excite the entire NMR spectrum.

Applying such a pulse to a set of nuclear spins simultaneously excites all the single-quantum NMR transitions. In terms of the net magnetization vector, this corresponds to tilting the magnetization vector away from its equilibrium position (aligned along the external magnetic field). The out-of-equilibrium magnetization vector precesses about the external magnetic field vector at the NMR frequency of the spins. This oscillating magnetization vector induces a current in a nearby pickup coil, creating an electrical signal oscillating at the NMR frequency. This signal is known as the free induction decay (FID) and contains the vector-sum of the NMR responses from all the excited spins. In order to obtain the frequency-domain NMR spectrum (NMR absorption intensity vs. NMR frequency) this time-domain signal (intensity vs. time) must be FTed. Fortunately the development of FT NMR coincided with the development of digital computers and Fast Fourier Transform algorithms. FT methods can be applied to many types of spectroscopy; see the general article on Fourier transform spectroscopy.

Richard R. Ernst was one of the pioneers of pulse (FT) NMR and won a Nobel Prize in chemistry in 1991 for his work on FT NMR and his development of multi-dimensional NMR (see below).

Multi-dimensional NMR Spectroscopy

The use of pulses of different shapes, frequencies and durations in specifically-designed patterns or pulse sequences allows the spectroscopist to extract many different types of information about the molecule. Multi-dimensional nuclear magnetic resonance spectroscopy is a kind of FT NMR in which there are at least two pulses and, as the experiment is repeated, the pulse sequence is varied. In multidimensional nuclear magnetic resonance there will be a sequence of pulses and, at least, one variable time period. In three dimensions, two time sequences will be varied. In four dimensions, three will be varied.

There are many such experiments. In one, these time intervals allow (amongst other things) magnetization transfer between nuclei and, therefore, the detection of the kinds of nuclear-nuclear interactions that allowed for the magnetization transfer. Interactions that can be detected are usually classified into two kinds. There are through-bond interactions and through-space interactions, the latter usually being a consequence of the nuclear Overhauser effect. Experiments of the nuclear Overhauser variety may be employed to establish distances between atoms, as for example by 2D-FT NMR of molecules in solution.

Although the fundamental concept of 2D-FT NMR was proposed by Jean Jeener from the Free University of Brussels at an International Conference, this idea was largely developed by Richard Ernst who won the 1991 Nobel prize in Chemistry for his work in FT NMR, including multi-dimensional FT NMR, and especially 2D-FT NMR of small molecules.[8] Multi-dimensional FT NMR experiments were then further developed into powerful methodologies for studying biomolecules in solution, in particular for the determination of the structure of biopolymers such as proteins or even small nucleic acids.[9]

Kurt Wüthrich shared (with John B. Fenn) in 2002 the Nobel Prize in Chemistry for his work in protein FT NMR in solution.

Solid-state NMR spectroscopy

This technique complements biopolymer X-ray crystallography in that it is frequently applicable to biomolecules in a liquid or liquid crystal phase, whereas crystallography, as the name implies, is performed on molecules in a solid phase. Though nuclear magnetic resonance is used to study solids, extensive atomic-level biomolecular structural detail is especially challenging to obtain in the solid state. There is little signal averaging by thermal motion in the solid state, where most molecules can only undergo restricted vibrations and rotations at room temperature, each in a slightly different electronic environment, therefore exhibiting a different NMR absorption peak. Such a variation in the electronic environment of the resonating nuclei results in a blurring of the observed spectra—which is often only a broad Gaussian band for non-quadrupolar spins in a solid- thus making the interpretation of such "dipolar" and "chemical shift anisotropy" (CSA) broadened spectra either very difficult or impossible.

Professor Raymond Andrew at Nottingham University in the UK pioneered the development of high-resolution solid-state nuclear magnetic resonance. He was the first to report the introduction of the MAS (magic angle sample spinning; MASS) technique that allowed him to achieve spectral resolution in solids sufficient to distinguish between chemical groups with either different chemical shifts or distinct Knight shifts. In MASS, the sample is spun at several kilohertz around an axis that makes the so-called magic angle θm (which is ~54.74°, where cos2θm = 1/3) with respect to the direction of the static magnetic field B0; as a result of such magic angle sample spinning, the chemical shift anisotropy bands are averaged to their corresponding average (isotropic) chemical shift values. The above expression involving cos2θm has its origin in a calculation that predicts the magnetic dipolar interaction effects to cancel out for the specific value of θm called the magic angle. One notes that correct alignment of the sample rotation axis as close as possible to θm is essential for cancelling out the dipolar interactions whose strength for angles sufficiently far from θm is usually greater than ~10 kHz for C-H bonds in solids, for example, and it is thus greater than their CSA values.

There are different angles for the sample spinning relative to the applied field for the averaging of quadrupole interactions and paramagnetic interactions, correspondingly ~30.6° and ~70.1°

A concept developed by Sven Hartmann and Erwin Hahn was utilized in transferring magnetization from protons to less sensitive nuclei (popularly known as cross-polarization) by M.G. Gibby, Alex Pines and John S. Waugh. Then, Jake Schaefer and Ed Stejskal demonstrated also the powerful use of cross-polarization under MASS conditions which is now routinely employed to detect low-abundance and low-sensitivity nuclei.

Sensitivity

Because the intensity of nuclear magnetic resonance signals and, hence, the sensitivity of the technique depends on the strength of the magnetic field the technique has also advanced over the decades with the development of more powerful magnets. Advances made in audio-visual technology have also improved the signal-generation and processing capabilities of newer machines.

As noted above, the sensitivity of nuclear magnetic resonance signals is also dependent on the presence of a magnetically-susceptible nuclide and, therefore, either on the natural abundance of such nuclides or on the ability of the experimentalist to artificially enrich the molecules, under study, with such nuclides. The most abundant naturally-occurring isotopes of hydrogen and phosphorus (for example) are both magnetically susceptible and readily useful for nuclear magnetic resonance spectroscopy. In contrast, carbon and nitrogen have useful isotopes but which occur only in very low natural abundance.

Other limitations on sensitivity arise from the quantum-mechanical nature of the phenomenon. For quantum states separated by energy equivalent to radio frequencies, thermal energy from the environment causes the populations of the states to be close to equal. Since incoming radiation is equally likely to cause stimulated emission (a transition from the upper to the lower state) as absorption, the NMR effect depends on an excess of nuclei in the lower states. Several factors can reduce sensitivity, including

Isotopes

Many chemical elements can be used for NMR analysis.[10]

Commonly used nuclei:

Other nuclei (usually used in the studies of their complexes and chemical binding, or to detect presence of the element):

  • 6Li, 7Li
  • 9Be
  • 19F
  • 21Ne
  • 23Na
  • 25Mg
  • 27Al
  • 29Si
  • 31P
  • 33S
  • 39K, 40K, 41K
  • 45Sc
  • 47Ti, 49Ti
  • 50V, 51V
  • 53Cr
  • 55Mn
  • 57Fe
  • 59Co
  • 61Ni
  • 63Cu, 65Cu
  • 67Zn
  • 69Ga, 71Ga
  • 73Ge
  • 77Se
  • 81Br
  • 87Rb
  • 87Sr
  • 95Mo
  • 109Ag
  • 113Cd
  • 119Sn
  • 125Te
  • 127I
  • 133Cs
  • 135Ba, 137Ba
  • 139La
  • 183W
  • 199Hg

Applications

Medicine

Medical MRI

The application of nuclear magnetic resonance best known to the general public is magnetic resonance imaging for medical diagnosis and MR Microscopy in research settings, however, it is also widely used in chemical studies, notably in NMR spectroscopy such as proton NMR, carbon-13 NMR, deuterium NMR and phosphorus-31 NMR. Biochemical information can also be obtained from living tissue (e.g. human brain tumors) with the technique known as in vivo magnetic resonance spectroscopy or chemical shift NMR Microscopy.

These studies are possible because nuclei are surrounded by orbiting electrons, which are charged particles that generate small, local magnetic fields that add to or subtract from the external magnetic field, and so will partially shield the nuclei. The amount of shielding depends on the exact local environment. For example, a hydrogen bonded to an oxygen will be shielded differently than a hydrogen bonded to a carbon atom. In addition, two hydrogen nuclei can interact via a process known as spin-spin coupling, if they are on the same molecule, which will split the lines of the spectra in a recognizable way.

As one of the two major spectroscopic techniques used in metabolomics, NMR is used to generate metabolic fingerprints from biological fluids to obtain information about disease states or toxic insults.

Chemistry

By studying the peaks of nuclear magnetic resonance spectra, chemists can determine the structure of many compounds. It can be a very selective technique, distinguishing among many atoms within a molecule or collection of molecules of the same type but which differ only in terms of their local chemical environment. See the articles on carbon-13 NMR and proton NMR for detailed discussions.

By studying T2*information, a chemist can determine the identity of a compound by comparing the observed nuclear precession frequencies to known frequencies. Further structural data can be elucidated by observing spin-spin coupling, a process by which the precession frequency of a nucleus can be influenced by the magnetization transfer from nearby nuclei. Spin-spin coupling is most commonly observed in NMR involving common isotopes, such as Hydrogen-1 (1H NMR).

Because the nuclear magnetic resonance timescale is rather slow, compared to other spectroscopic methods, changing the temperature of a T2*experiment can also give information about fast reactions, such as the Cope rearrangement or about structural dynamics, such as ring-flipping in cyclohexane. At low enough temperatures, a distinction can be made between the axial and equatorial hydrogens in cyclohexane.

An example of nuclear magnetic resonance being used in the determination of a structure is that of buckminsterfullerene (often called "buckyballs", composition C60). This now famous form of carbon has 60 carbon atoms forming a sphere. The carbon atoms are all in identical environments and so should see the same internal H field. Unfortunately, buckminsterfullerene contains no hydrogen and so 13C nuclear magnetic resonance has to be used. 13C spectra require longer acquisition times since carbon-13 is not the common isotope of carbon (unlike hydrogen, where 1H is the common isotope). However, in 1990 the spectrum was obtained by R. Taylor and co-workers at the University of Sussex and was found to contain a single peak, confirming the unusual structure of buckminsterfullerene.[11]

Non-destructive testing

Nuclear magnetic resonance is extremely useful for analyzing samples non-destructively. Radio waves and static magnetic fields easily penetrate many types of matter and anything that is not inherently ferromagnetic. For example, various expensive biological samples, such as nucleic acids, including RNA and DNA, or proteins, can be studied using nuclear magnetic resonance for weeks or months before using destructive biochemical experiments. This also makes nuclear magnetic resonance a good choice for analyzing dangerous samples.

Acquisition of dynamic information

In addition to providing static information on molecules by determining their 3D structures in solution, one of the remarkable advantages of NMR over X-ray crystallography is that it can be used to obtain important dynamic information including the low-frequency collective motion in proteins and DNA, for example in the Ca2+-calmodulin system.[12]. The low-frequency internal motion in biomacromolecules and its biological functions have been discussed by Chou.[13].

Data acquisition in the petroleum industry

Another use for nuclear magnetic resonance is data acquisition in the petroleum industry for petroleum and natural gas exploration and recovery. A borehole is drilled into rock and sedimentary strata into which nuclear magnetic resonance logging equipment is lowered. Nuclear magnetic resonance analysis of these boreholes is used to measure rock porosity, estimate permeability from pore size distribution and identify pore fluids (water, oil and gas). These instruments are typically low field NMR spectrometers.

Flow probes for NMR spectroscopy

Recently, real-time applications of NMR in liquid media have been developed using specifically designed flow probes (flow cell assemblies)which can replace standard tube probes. This has enabled techniques that can incorporate the use of high performance liquid chromatography (HPLC) or other continuous flow sample introduction devices.[14]

Process control

NMR has now entered the arena of real-time process control and process optimization in oil refineries and petrochemical plants. Two different types of NMR analysis are utilized to provide real time analysis of feeds and products in order to control and optimize unit operations. Time-domain NMR (TD-NMR) spectrometers operating at low field (2–20 MHz for 1H) yield free induction decay data that can be used to determine absolute hydrogen content values, rheological information, and component composition. These spectrometers are used in mining, polymer production, cosmetics and food manufacturing as well as coal analysis. High resolution FT-NMR spectrometers operating in the 60 MHz range with shielded permanent magnet systems yield high resolution 1H NMR spectra of refinery and petrochemical streams. The variation observed in these spectra with changing physical and chemical properties is modeled using chemometrics to yield predictions on unknown samples. The prediction results are provided to control systems via analogue or digital outputs from the spectrometer.

Earth's field NMR

In the Earth's magnetic field, NMR frequencies are in the audio frequency range, or the very low frequency band of the radio frequency spectrum. Earth's field NMR (EFNMR) is typically stimulated by applying a relatively strong dc magnetic field pulse to the sample and, following the pulse, analyzing the resulting low frequency alternating magnetic field that occurs in the Earth's magnetic field due to free induction decay (FID). These effects are exploited in some types of magnetometers, EFNMR spectrometers, and MRI imagers. Their inexpensive portable nature makes these instruments valuable for field use and for teaching the principles of NMR and MRI.

Quantum computing

NMR quantum computing uses the spin states of molecules as qubits. NMR differs from other implementations of quantum computers in that it uses an ensemble of systems, in this case molecules. The ensemble is initialized to be the thermal equilibrium state (see quantum statistical mechanics).

Magnetometers

Main article: Magnetometer

Various magnetometers use NMR effects to measure magnetic fields, including proton precession magnetometers (PPM) (also known as proton magnetometers), and Overhauser magnetometers. See also Earth's field NMR.

Makers of NMR equipment

Major NMR instrument makers include Oxford Instruments, Bruker, Spinlock SRL, General Electric, JEOL, Kimble Chase, Philips, Siemens AG and Varian, Inc..

See also

  • Carbon-13 NMR
  • Chemical shift
  • Dynamic nuclear polarisation (DNP)
  • Earth's field NMR (EFNMR)
  • Free induction decay (FID)
  • In vivo magnetic resonance spectroscopy (MRS)
  • J-coupling
  • Larmor equation (Not to be confused with Larmor formula).
  • Larmor precession
  • Low field NMR
  • Magic angle spinning
  • Magnetometer
  • Magnetic resonance imaging (MRI)
  • NMR spectra database
  • NMR spectroscopy
  • NMR Microscopy
  • Nuclear magnetic resonance in porous media
  • Nuclear quadrupole resonance (NQR)
  • Protein dynamics
  • Protein NMR
  • Proton NMR
  • Rabi cycle
  • Relaxometry
  • Relaxation (NMR)
  • Solid-state NMR
  • Zero field NMR

Notes

  1. ↑ I.I. Rabi, J.R. Zacharias, S. Millman, P. Kusch (1938). "A New Method of Measuring Nuclear Magnetic Moment". Physical Review 53: 318. doi:10.1103/PhysRev.53.318. 
  2. ↑ Biography of I. Rabi at Nobelprize.org
  3. ↑ Filler, Aaron (2009). "The History, Development and Impact of Computed Imaging in Neurological Diagnosis and Neurosurgery: CT, MRI, and DTI". Nature Precedings. doi:10.1038/npre.2009.3267.5. 
  4. ↑ I.C. Baianu, K.A. Rubinson, J. Patterson (1979). "Ferromagnetic Resonance and Spin Wave Excitations in Metallic Glasses". J. Phys. Chem. Solids 40 (12): 941–950. doi:10.1016/0022-3697(79)90122-7. 
  5. ↑ I.C. Baianu (1979). "Ferromagnetic resonance and spin wave excitations in metallic glasses: The effects of thermal ageing and long-range magnetic ordering". Solid State Communications 29: i–xvi. doi:10.1016/0038-1098(79)91190-6. 
  6. ↑ Quantum automaton and quantum computation (see also references therein)
  7. ↑ Rabi, I. I.; Zacharias, J.; Millman, S.; Kusch, P. (1938). "A New Method of Measuring Nuclear Magnetic Moment". Physical Review 53 (1): 318. doi:10.1103/PhysRev.53.318. PMID 9981980. 
  8. ↑ "Nuclear Magnetic Resonance Fourier Transform Spectroscopy" Ernst's Nobel lecture. (Includes mention of Jeener's suggestion.)
  9. ↑ I.C. Baianu. "Two-dimensional Fourier transforms". 2D-FT NMR and MRI. PlanetMath. http://planetmath.org/encyclopedia/TwoDimensionalFourierTransforms.html. Retrieved 2009-02-22. 
  10. ↑ Multinuclear NMR
  11. ↑ R. Taylor, J.P. Hare, A.K. Abdul-Sada, H.W. Kroto (1990). "Isolation, separation and characterization of the fullerenes C60 and C70: the third form of carbon". Journal of the Chemical Society, Chemical Communications 20: 1423–1425. doi:10.1039/c39900001423. 
  12. ↑ Chou, J. J., Li, S., Klee, C. B. & Bax, A. (2001). Solution structure of Ca2+-calmodulin reveals flexible hand-like properties of its domains. Nature Structural Biology 8, 990-997.
  13. ↑ Kuo-Chen Chou (1988) Low-frequency collective motion in biomacromolecules and its biological functions. Biophys Chem 30, 3-48.
  14. ↑ R.L Haner and P.A, Keifer (2009). "Flow Probes for NMR Spectroscopy". Encyclopedia of Magnetic Resonance. doi:10.1002/9780470034590.emrstm1085. 

References

External links

Tutorial

Animations and Simulations

Software

Video

Forums

Wiki